- Les oppgavebeskrivelsen her: oppgaver-uke-34.pdf
- Last ned programmet SPSS her
- Finn datafilene (og annen informasjon) her: vo2.sav og vo2hr.sav
- Eventuelt titte på instruksjonshåndboken her
Oppgave 1 (kopiert rett fra oppgavefilen)
Vi skal introdusere et datamateriale, som også stammer fra University of Massachusetts. Det er til sammen data fra 233 menn (individ 139 mangler) som deltok i en undersøkelse av fysisk form og oksygenopptak under arbeid. En del av undersøkelsen ble foretatt på tredemølle hvor O2-opptak og blodtrykk ble målt.
De viktige variablene er maksimalt O2- opptak på tredemøllen (VO2, målt i ml/kg/min) og
Aerob svekkelse (FAI, målt i prosent relativt til alder og kjønn). VO2 er maksimum antall
milliliter av oksygen opptatt i løpet av 1 minutt, per kg kroppsvekt.
På nettet finnes det en rekke enkle kalkulatorer på av maksimalt O2- opptak – uten å løpe på tredemølle, se for eksempel https://www.ntnu.no/cerg/vo2max.
Det er ingen Missing values på datafilen
Løsning oppgave 1
3. Lag en deskriptiv analyse av VO2. Gjør dette via Analyze/Descriptive Statistics/Explore.
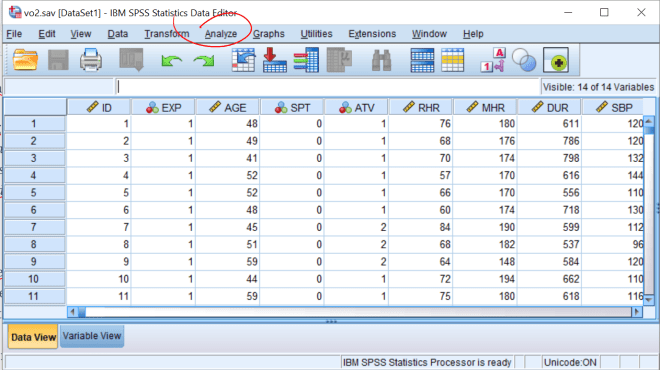
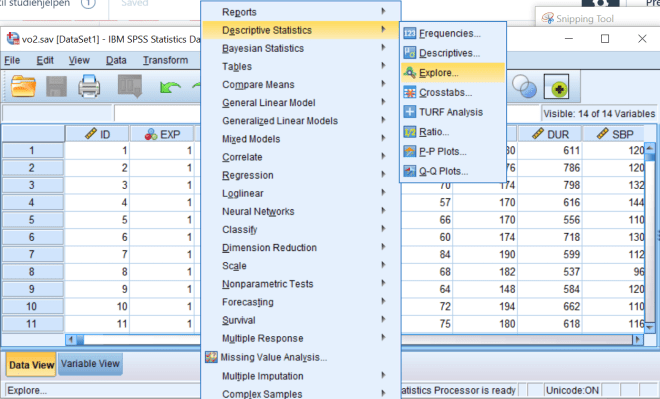
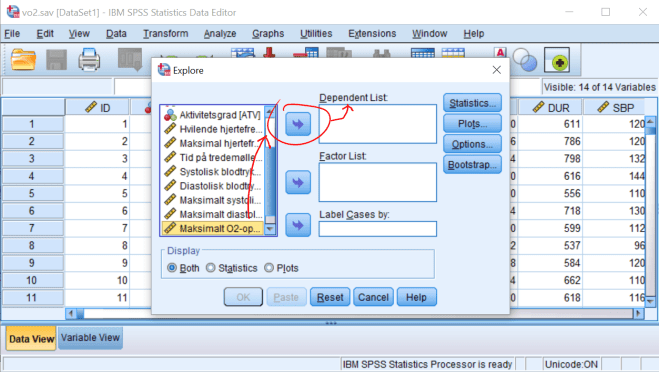
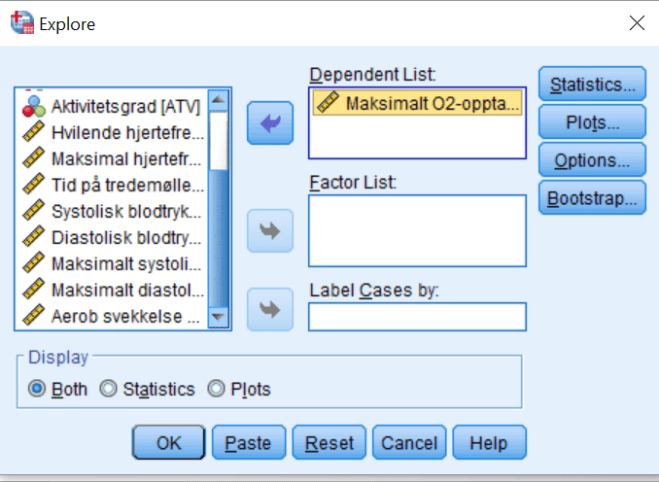

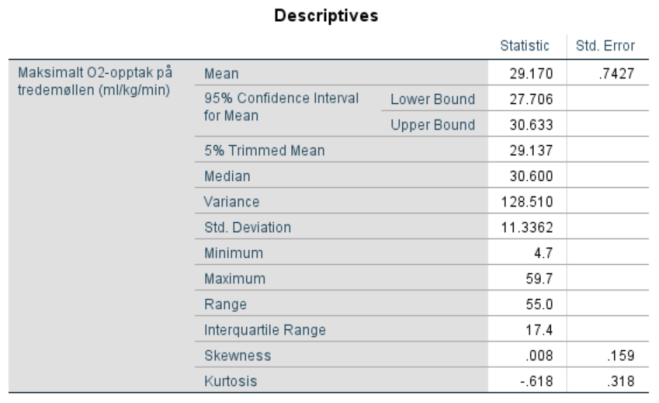
Forklar hva gjennomsnittene, medianene, standardavvikene og standardfeilen til gjennomsnittet (Std. Error) uttrykker. Forklar boksplottene.
- Gjennomsnittet
Sum av observasjoner / antall observasjoner.
- Medianen
Like mange observasjoner over som under medianobservasjonen. Om antall observasjoner er et partall, blir medianverdien vanligvis et gjennomsnitt av de to midterste verdiene.
- Standardavviket
Verdienes gjennomsnittsavstand fra gjennomsnittsverdien
- Standardfeilen
Standardavviket / kvadratroten av antall observasjoner. Hva ligger bak formelen? La oss si at det snart er stortingsvalg. Avisene tar en meningsmåling (typisk grupper på 1000) som viser at 23% stemmer på Høyre. I en annen måling med en annen gruppe mennesker får vi kanskje 26%. Jo flere målinger vi tar av grupper på 1000, jo nærmere kommer vi populasjonsverdien (altså den egentlige prosentverdien for hele befolkningen). Standardavviket til alle disse “småverdiene” kaller vi da for standardfeilen, altså graden av usikkerhet i meningsmålingene.
- Interkvartil avstand
Deler målingene i fire grupper. Når første 25% av målingene er bak oss kaller vi det for første kvartil. Like så kalles 50% for andre kvartil (eller medianen) og 75% for tredje kvartil. Avstanden mellom første og tredje kvartil kaller vi den interkvartile avstanden. I praksis har vi da med 50% av målingene.
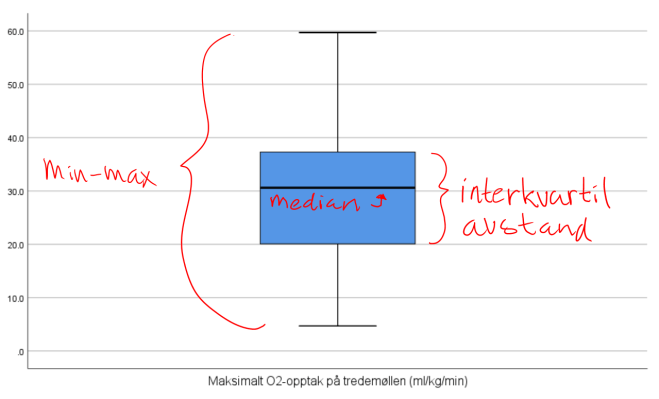
Figuren ovenfor kaller vi et boksplott og er en grafisk fremstilling av noen utvalgte deskriptive verdier.
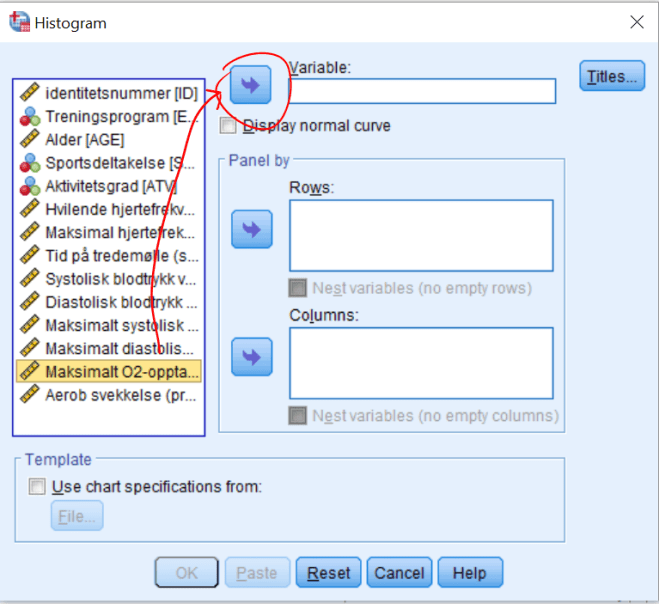

Jo flere observasjoner, jo nærmere kommer vi en kurve (og en sannsynlighetsfordeling). Den mest brukte sannsynlighetsfordelingen er en normalfordeling som er symmetrisk rundt gjennomsnittet. Det er ofte interessant å se på hvordan målinger samsvarer med en normalfordeling. Dette kan vi sjekke ved:


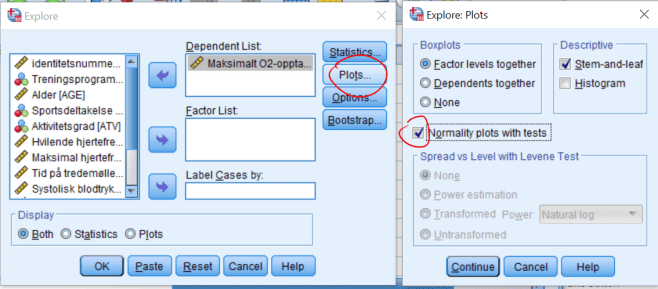
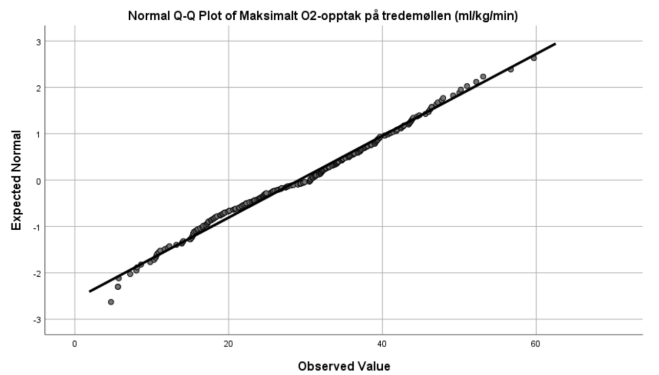
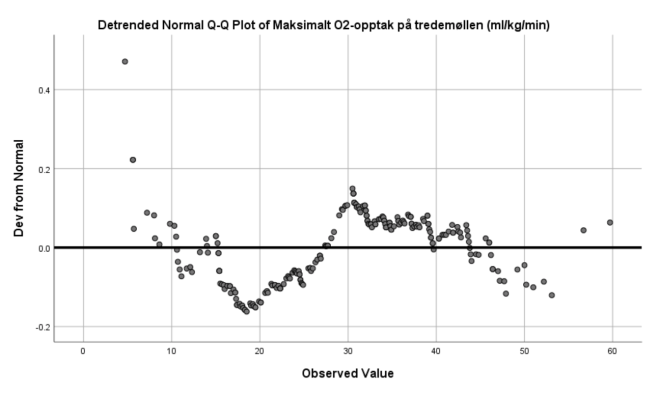
Jo nærmere verdiene er normalfordelte, jo mer samsvarer de med grafene (hvor stor andel som ligger innen normalfordelingen). I praksis vil vi aldri se reelle data som ligger eksakt på normalfordeligen. Foreleser forteller at han selv aldri har klart å tolke den horisontale grafen langs x. Da er det vel trygt å anta at dette heller ikke er pensum (med mindre det er ekstreme avvik eller samsvarelser).
For å undersøke om VO2 er normalfordelt skal vi laget et normalfordelingsplott. Da går vi tilbake til Analyze/Descriptive Statistics/Explore, og vi klikker på Plots i den høyre knapperekken. Da åpner det seg en ny meny. Der klikker vi på Normality plots with tests. Kan vi anta at VO2 er normalfordelt?
Nei.
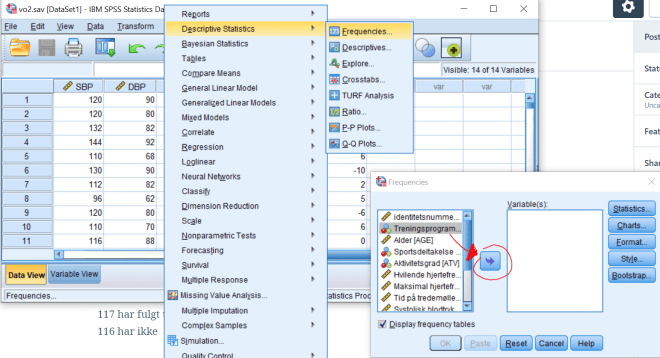
Lag en frekvensfordeling for variabelen EXP. Gjør dette via Analyze/Descriptives/Frequencies. Forklar resultatene.

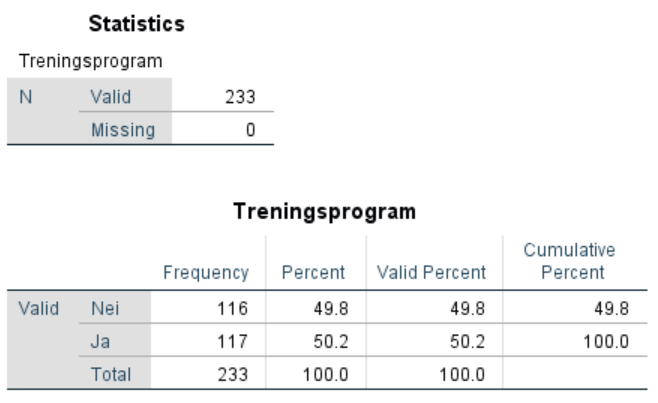
Vi ser her at 117 har fulgt treningsprogrammet og 116 ikke. Når vi har en så jevn fordeling er det naturlig å tenke seg at det ikke er et tilfeldig oppsett, men en designet studie (at halvparten f.eks. har fått et treningsprogram, halvparten ikke).
To prosenter
- Precent
Prosentandel av alle svarene
- Valid precent
Prosentandel av alle gyldige svar, dvs. ikke talt med “missing values”
Når det er snakk om kategoriske variabler med mange kategorier, f.eks. fødeland, kan det være naturlig å oppsummere det i et stolpediagram.
6. Variabelen FAI er en kontinuerlig variabel som angir graden av aerob svekkelse. Hvis FAI er større eller lik 0 er personen aerob svekket, er FAI mindre enn 0 er personen ikke svekket. Vi skal lage en variabel IMP som angir om personen er svekket eller ikke. Lag da variabelen:
- IMP = 1 når FAI >= 0
- IMP = 0 når FAI < 0

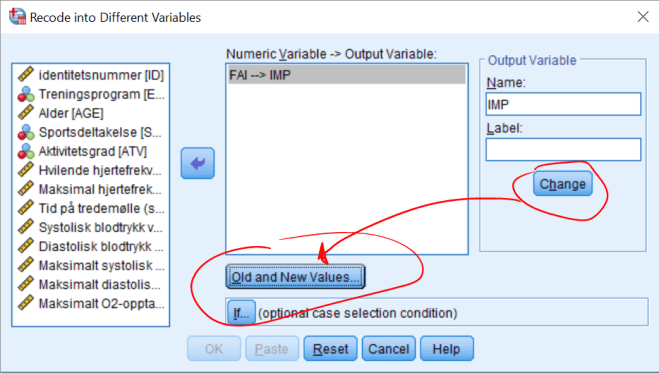
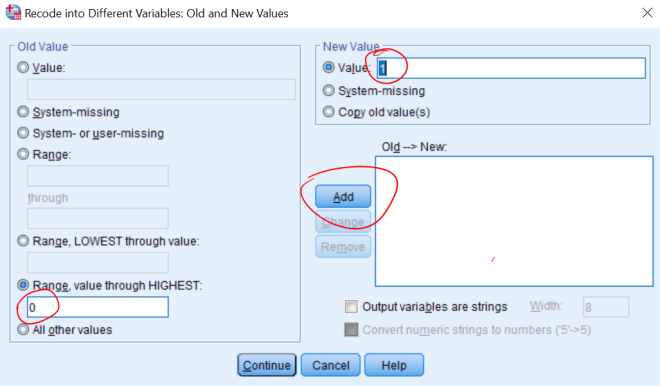
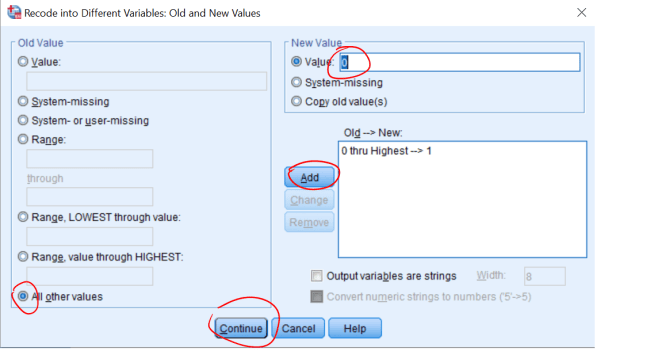
Vi velger ikke “Range, LOWEST through value”, for da tar vi med 0 i begge omganger. Om det finnes “missing values” i datasettet “prikker vi av” “System-missing”-alternativet. Manglende verdier ser ut i datafilen som et åpent felt, men er kodet som en ekstremverdi (enten ekstremt høy eller lav). Disse verdiene tas med dersom vi f.eks. har alle verdier fra 0 og oppover og kan påvirke resultatene vi får. Det kan være lurt å gi den nye variabelen et “label”, f.eks. “Svekkelse”
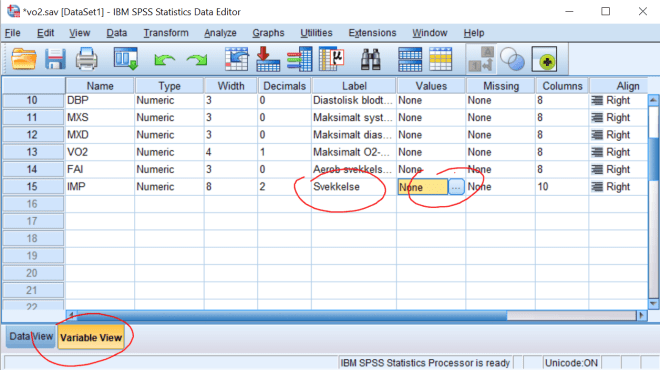
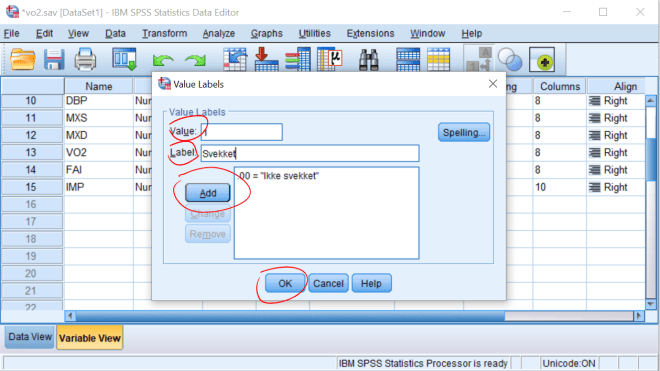
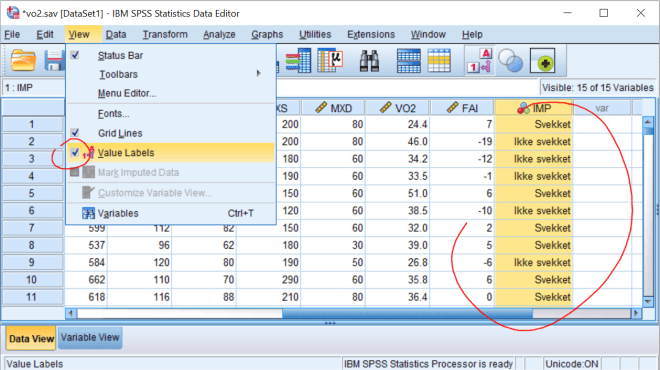
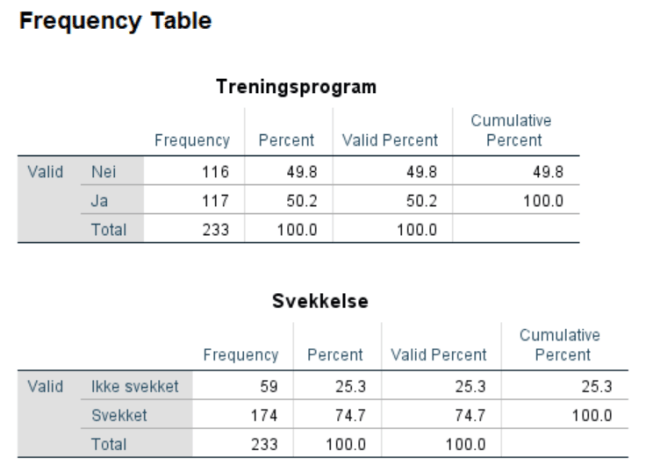
Lag frekvenstabell som tidligere. Vi ser her at et overveiende flertall opplever å bli svekket (59 v. 174).
9. Lag en deskriptiv analyse av VO2 mht. til IMP. Meningen er da å gi en presentasjon av de sentrale målene, som gjennomsnitt, median, standardavvik etc. for VO2 for de to gruppene av IMP. Gjør dette via Analyze/Descriptive Statistics/Explore. Hva er gjennomsnittene, medianene, standardavvikene og standardfeilen til gjennomsnittet (Std. Error)? Forklar boksplottene.
Det er litt merkelig å undersøke disse forholdene da IMP er basert på VO2 (men la gå).


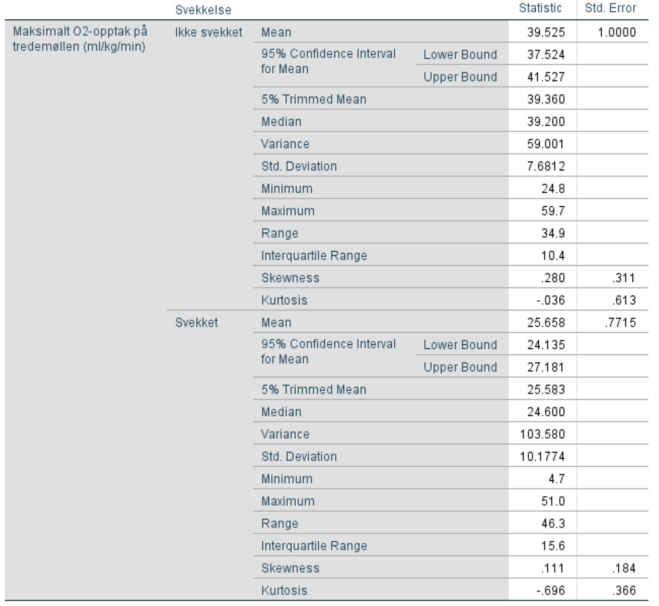
Observer at det er en forskjell på feilmarginen “Std. Error” mellom gruppen som er svekket (0.7715) og ikke svekket (1.0000). Grunnen til det er fordi vi regner ut feilmarginen ved formelen: standardavvik/roten av antall observasjoner. Hva det vil si i praksis er at det rett og slett er flere som opplever å bli svekket enn ikke.
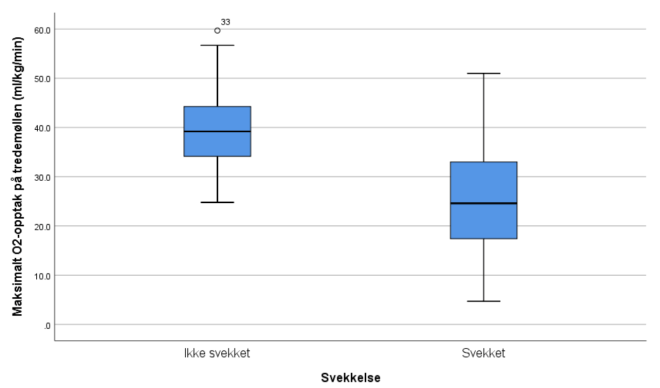
Boksplottet
- Mindre spredning (interkvartil avstand, min-max) blant gruppen “ikke svekket”
- Generelt høyere VO2 for “ikke svekket”
Merk at SPSS har satt ring rundt og skrevet “33” over boksplottet til “ikke svekket” Det er fordi programmet vil understreke at observasjon #33 er i overkant stor (i forhold til normen). Observasjon 33 har VO2-verdien: 59.7 som nærmer seg opptaket til en eliteutøver. Når SPSS skisserer boksplottene gjør de en antagelse om at datasettet er normalfordelt. Observasjoner som er lengre unna gjennomsnittsverdien enn et gitt antall standardavvik markeres automatisk av programmet.
Oppgave 2 (bytte til vo2hr.sav)
Kroppen opptar mer oksygen under arbeid enn under hvile, og for å transportere oksygen til musklene må hjertet slå fortere. Hjertefrekvens er lett å måle, mens oksygenopptaket er vanskeligere. Denne studien er basert på 38 arbeidere. Vi skal studere to arbeidsbetingelser, i det arbeidet er utført med og uten beskyttende arbeidsmaske. Arbeidet er av 19 arbeidere utført uten beskyttende ansiktsmaske og for 19 andre arbeidere er det utført med ansiktsmaske. Målsetningen i studien er å se om det er en sammenheng mellom oksygenopptak (VO2) og hjertefrekvens (HR) for de to arbeidsbetingelsene. Basert på dataene nedenfor skal vi undersøke om dette virker rimelig.
Merk ummidelbart at studieutvalget er svært lite og eventuelle konklusjoner dermed svekkede.
Relevant informasjon:
- To faktorer:
Hjertefrekvens (HR)
Oksygenopptak (VO2)
- Med og uten maske
- 38 arbeidere

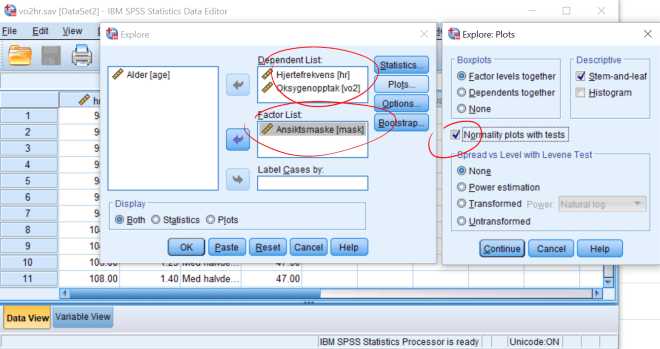
 4. Lag boksplott for VO2 og HR for personer med og uten bruk av ansiktsmaske. Forklar hva du finner. Er fordelingen til disse to variablene symmetriske?
4. Lag boksplott for VO2 og HR for personer med og uten bruk av ansiktsmaske. Forklar hva du finner. Er fordelingen til disse to variablene symmetriske?
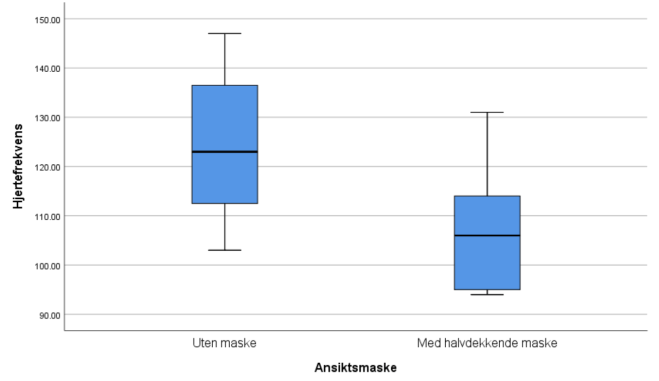
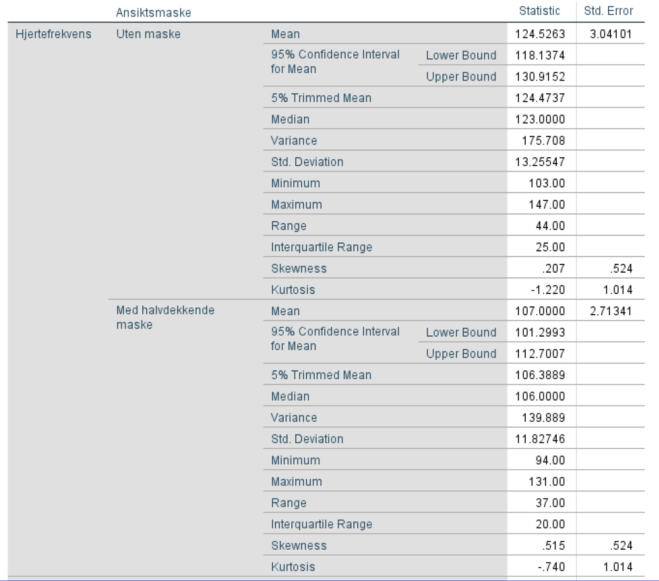
- HR uten maske
Vi ser at boksplottet er relativt symmetrisk. Avstandene fra min og max til medianen er ~like. Avstanden fra 1. til 2. (medianen) og 3. til 2. (medianen) kvartil er ganske lik.
- HR med maske
Vi ser her at boksplottet er relativt usymmetrisk. Selv om avstanden fra 1. til 2. (medianen) og 3. til 2. kvartil (medianen) er ganske lik, er det stor forskjell på avstandene fra min og max til medianen (og den interkvartile avstanden). Det kan være fordi studieutvalget er for lite.
Sammenligning
Boksplottene viser en tydelig redusert hjertefrekvens for de som hadde på seg maske.
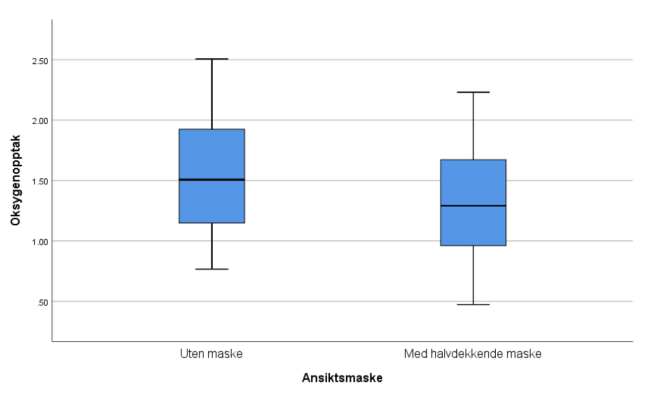
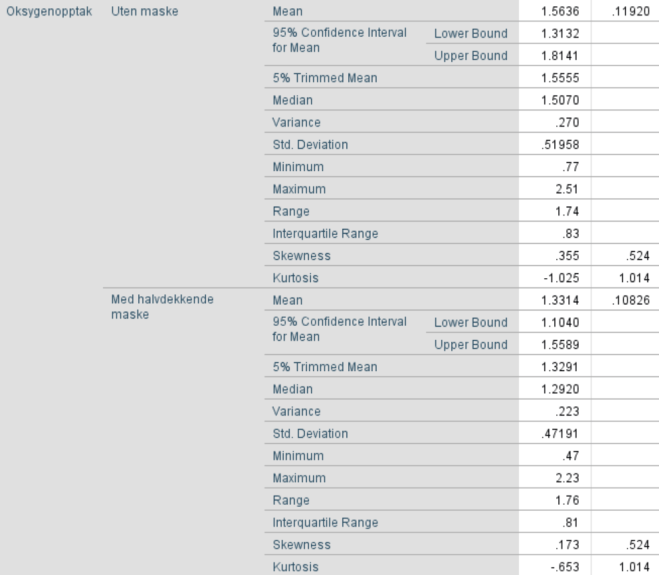
- VO2-opptak uten maske
Vi ser at boksplottet er relativt symmetrisk. Avstandene fra min og max til medianen er ~like. Avstanden fra 1. til 2. (medianen) og 3. til 2. (medianen) kvartil er ganske lik.
- VO2-opptak med maske
Vi ser at boksplottet er relativt symmetrisk. Avstandene fra min og max til medianen er ~like. Avstanden fra 1. til 2. (medianen) og 3. til 2. (medianen) kvartil er ganske lik.
Sammenligning
Boksplottene viser noe lavere VO2-opptak med maske på. Det er naturlig da masken gjør det vanskeligere å puste.
Tolkning
Resultatene tyder på at det er en assosiasjon mellom maskebruk og både redusert VO2-opptak og hjertefrekvens. En konfunderende faktor kunne vært arbeidsintensitet. Resultatene kan f.eks. forklares ved at de som hadde på seg maske som gjorde det vanskeligere å puste jobbet mindre intenst og viste dermed også lavere hjertefrekvens.
5. Lag normalfordelingsplott for VO2 og HR for personer med og uten bruk av ansiktsmaske. Hva finner du?
Datamengdene samsvarer ikke med en normalfordeling.
Lag et spredningsdiagram for sammenhengen mellom VO2 og HR for dem med og uten ansiktsmaske, med VO2 på y-aksen og HR på x-aksen. Det gjør vi ved å gå til Graphs/Legacy Dialogs/Scatter/Dots. Her klikker vi på Simple Scatter og Define. Vi trekker VO2 over i y-aksen og HR over i x-aksen og MASK over i Set Markers by.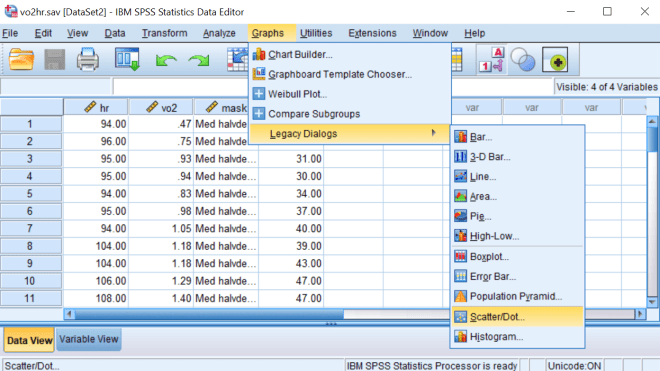

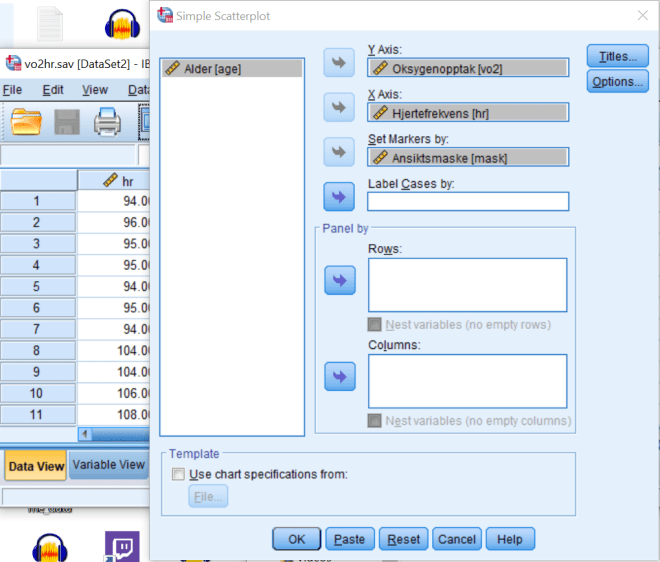
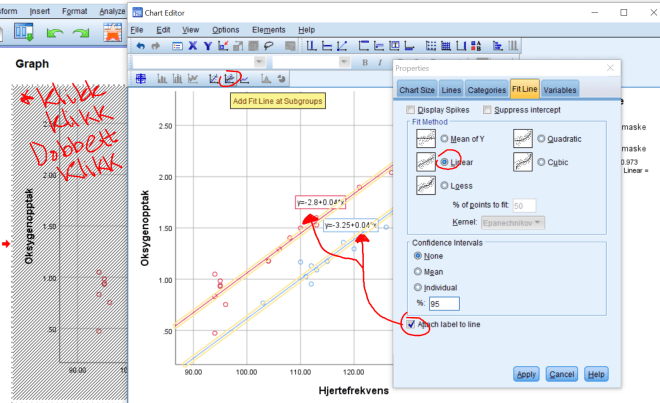
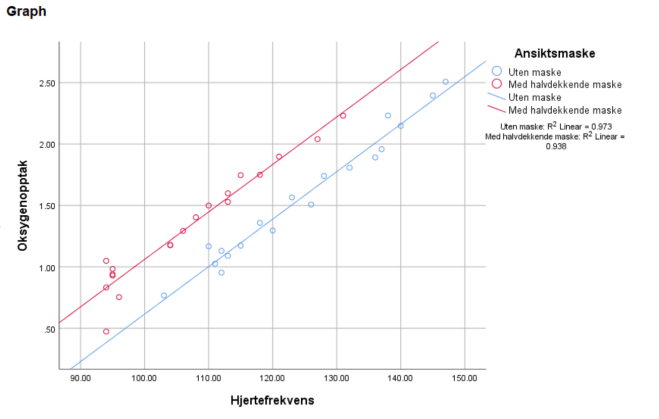 Det at grafene (regresjonslinjene) er tilnærmet parallelle betyr at veksten (proporsjonalitetskonstanten a i y=ax+b) er ~lik. Grunnen til at grafene er forskjøvet er fordi oksygenopptaket er generelt lavere med maske på (gir mening i praksis!).
Det at grafene (regresjonslinjene) er tilnærmet parallelle betyr at veksten (proporsjonalitetskonstanten a i y=ax+b) er ~lik. Grunnen til at grafene er forskjøvet er fordi oksygenopptaket er generelt lavere med maske på (gir mening i praksis!).
8. Forklar sammenhengen mellom oksygenopptak og hjertefrekvens ut fra resultatene fra denne studien.
Vi ser fra regresjonsplottet at forholdet mellom hjertefrekvens (HF) og oksygenopptak (VO2) er tilnærmet konstant uavhengig av faktorer som reduserer oksygentilgangen (maske). Er studien fullstendig konkluderende? Det er de aldri, men ideelt sett kunne vi gjort målingene på nytt med et større utvalg.
Foreleser: Morten Valberg



































 4. Lag boksplott for VO2 og HR for personer med og uten bruk av ansiktsmaske. Forklar hva du finner. Er fordelingen til disse to variablene symmetriske?
4. Lag boksplott for VO2 og HR for personer med og uten bruk av ansiktsmaske. Forklar hva du finner. Er fordelingen til disse to variablene symmetriske?





 Det at grafene (regresjonslinjene) er tilnærmet parallelle betyr at veksten (proporsjonalitetskonstanten a i y=ax+b) er ~lik. Grunnen til at grafene er forskjøvet er fordi oksygenopptaket er generelt lavere med maske på (gir mening i praksis!).
Det at grafene (regresjonslinjene) er tilnærmet parallelle betyr at veksten (proporsjonalitetskonstanten a i y=ax+b) er ~lik. Grunnen til at grafene er forskjøvet er fordi oksygenopptaket er generelt lavere med maske på (gir mening i praksis!).