Descartes hadde en teori om at vi skulle kunne bruke matematikken som et språk for å beskrive all vitenskap. Den nye fysikken vi ser i dag er inspirert av denne ideen.
Tanker som kjennetegner Descartes:
Rasjonalisme
Fornuft, ikke erfaring, er kilden til sikker erkjennelse. Vi kan finne fram til visse sannheter bare ved hjelp av tankene.
Dualisme
Teorien om at det finnes to fundamentalt forskjellige typer ting eller prinsipper. To legemer: det materielle og det åndelige (tenkende). Mennesket består av en dualisme av disse.
Kartesiansk, kartesisk
Descartes er så berømt at han har gitt navn til et eget adjektiv. Begrepet brukes om et dualistisk syn på mennesket og dets forhold til den ytre verdenen.
Et av hans mest berømte tankeeksperimenter begynte da han en dag oppdaget at mye av det han tidligere anså som sannhet senere hadde vist seg for å være feil. Dersom grunnlaget var feil, mente han at all kunnskap han senere hadde tilegnet seg også måtte være det. Han bestemte seg derfor for å gjøre alt på nytt og rydde opp i tankene. Metoden han valgte var å betvile alt.
Hva kan betviles?
- Illusjonsargumentet
Umiddelbare sanseerfaringer kan betviles. Det er ikke lurt å stole blindt på de ting som tidligere har bedratt oss. - Drømmeargumentet
Drøm og våken tilstand kan ikke skjelnes mellom. - Ond-ånd-argumentet
Alt du oppfatter kan være fabrikert av en ond ånd.
Etter at Descartes hadde betvilt alt, satte han igjen med konklusjonen at det eneste han visste med sikkerhet var at han tenkte, altså: cogito ergo sum, på fransk: je pense, donc je suis.
Finnes det typer kunnskap som er sikrere enn andre?
Descartes mente svaret på dette spørsmålet var vitenskaper som matematikk, geometri usw. som handlet om å forstå byggesteinene verdenen består av.
Det eneste han hadde helt sikker kunnskap om var “res cogitans”, at han var en tenkende ting. Kroppen, det fysiske, kunne for all del være en illusjon.
Syllogistisk tolkning:
- Alle tenkende ting eksisterer
- Jeg tenker
- Derfor eksisterer jeg
Dette avvises i AT140-141
Intuitiv tolkning (AT422)
Jeg har en umiddelbar intuisjon av min egen eksistens når jeg tenker. Tanker flyter ikke bare rundt. Alle tanker har en tenker.
Han oppnår ved den hyperbole tvilen:
- En sannhet han er helt sikker på (AT25, Exphil I s. 82).
- Å fokusere oppmerksometen sin på ren tenkning som en kilde til sikkerhet (AT28-29, Exphil I, s. 84).
- En standard for sikkerhet med klar og tydelig persepsjon (AT 35-36).
En monolog
Hva mente jeg tidligere at jeg var?
Uten tvil et menneske.
Men hva er et menneske? Et tenkende dyr?
Slett ikke.
Jeg er da altså bare noe tenkende (res cogitans), dvs. ånd eller sjel, intellekt, fornuft.
Descartes bryter med Aristoteles som mente at det som finnes stort sett viser seg som det er, i.e. her er det dyr –> jeg er ett av dyrene –> det som karakteriserer meg er at jeg tenker. Descartes satte tvil ved det fysiske. Er jeg et menneske eller dyr? Det kan jeg ikke, uten tvil, konkludere.
Vokseksempelet
Hva er kilden til god erkjennelse? Hvordan vet man noe?
La oss ta for oss en klump med voks.
Hvordan kan vi vite at det er voks?
Forklaringskandidater
- Sansning
Du føler og ser at det er voks - Innbilningsevnen
Du innbiller deg at det er voks
MEN
Kan vi innbille alle mulige måter voks kan være på? Har vi fantasi nok til å innbille oss alle interaksjonene voks kan ha? Nei, mener Descartes. - Fornuften
Vi har kunnskap om at det er voks via. fornuften.
Etter å ha kommet fram til “cogito ergo sum”, forkaster han den hyperbole tvilen. Formålet hans var bare å finne kriterier for sikker kunnskap, altså fornuftsbasert kunnskap. Han akter ikke å bevise at hele verdenen finnes.
Jeg, dyr, maskiner
Det er tanken som avslører at vi er annerledes fra dyr. Språket avslører fornuften og er dens ytre indikasjon. Sansene i seg selv blir ikke kunnskap. Det er først når fornuften begriper og tolker dem at mennesket evner å forstå.
Foreleser: Ingvild Torsen






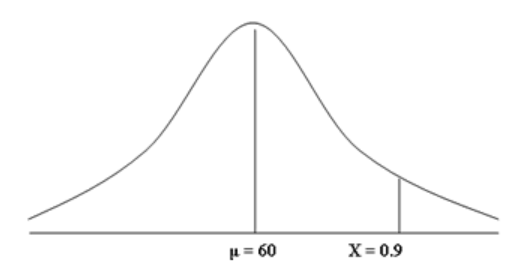
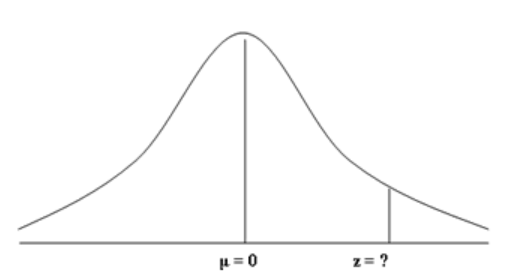



 Bruk sannsynlighetsregnereglene vi har lært til å svare på følgende spørsmål:
Bruk sannsynlighetsregnereglene vi har lært til å svare på følgende spørsmål: