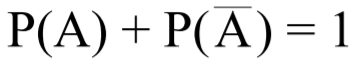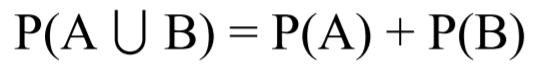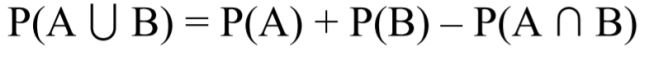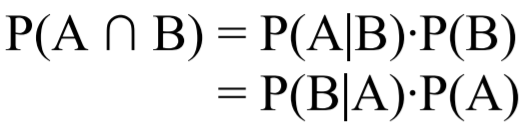sannsynlighet – Velkommen til studiehjelpen

Analyse av pardata: ett-utvalgs t-test

Fortsettelse fra sist
Vi kan ikke gi en fornuftig fortolkning av relativ risiko: 0.64 (36% redusert risiko) uten å vite hvilke tall som ligger bak. Om vi regner på risikodifferansen, finner vi at den er 1%. Forsøket i eksempelet vårt ble stoppet fordi forskerne mente det ikke lenger var forsvarlig å la pasienter stå på placebo. I en større samfunnsgruppe er det hensiktsmessig å se på RR (36%) da selv en liten endring i den reelle risikodifferansen kan utgjøre en forskjell for mange når populasjonen er stor.

Dilemma:
Er det forsvarlig å la en pasient stå / starte en pasient på medikamenter som gjør at en risiko går fra 3% til 2%, men som vedkommende må ta hele livet?

Ny kunnskap
Om vi har et normalfordelt utvalg vil gjennomsnittet også være normalfordelt.
E(X) = μ
SE(X) = σ / sqrt(n)

SE har samme funksjon som SD ved gjennomsnitt. Vi bruker SE ved estimator, SD ved datamengde.

Vi estimerer sigma (empirisk standardavvik) ved s = sqrt(1/(n-1) * sigma(xi-x)^2). Når vi estimerer sigma får vi naturligvis mer usikkerhet og derfor et bredere konfidensintervall (avhengig av størrelse på datamengde da s nærmer seg σ når n blir stor). Vi kan derfor ikke lenger bruke 1.96 som konstant, men en faktor c fra studentfordelingen (t-fordelingen). Den nye formelen blir da x +- c * s/sqrt(n). S er det empiriske standardavviket. Det finnes mange t-fordelinger. Utseende på dem varierer med antall frihetsgrader. Fordi studentfordelingen har mer usikkerhet, har sannsynlighetstettheten tyngre haler (tar for seg flere verdier utover i begge retninger). Vi må derfor litt lenger ut for å ta for oss 95% (derfor C >= 1.96). Vi regner ut antall frihetsgrader ved n – 1.

T-tabellen viser sannsynligheter for å overstige. Vi leser av 0.025 for å få et 0.05 α-nivå (tosidig). Fra presentasjon: “[…] siden vi skal ha 2.5% over verdien c og tilsvarende 2.5%
under verdien –c.” Vi forkaster H0 dersom verdien overstiger α-nivåverdien. Kjikvadratfordelingen er annerledes ved at vi ikke beregner noe konfidensintervall (gir oss direkte et svar).

Labtester vil ofte oppgi sin sigma, men i praksis må vi nesten alltid estimere den som s. Dersom vi forkaster H0 ved t-test, vil nullverdien (H0) aldri være inkludert i konfidensintervallet. Ved RR, kjikvadrat usw. kan det hende vi finner en/et overlapp.

Foreleser:
Det er ikke krise om den eksplisitte frihetsgraden ikke er gitt i tabellen. Forskjellene når vi får store frihetsgrader blir så små at de egentlig ikke har en stor praktisk betydning (innenfor våre rammer). “Bare begrunn valget.”

Notiser:
En paret t-test er bare en ett-utvalgs t-test på forskjellen mellom de to avhengige datasettene. Vi antar at standardavvikene i de opprinnelige datasettene er ~like. Standardavviket til forskjellene må nødvendigvis være mellom de to opprinnelige. SPSS tester om vi kan anta et tilstrekkelig likt standardavvik, men foreleser sier han ikke pleier å titte på den (dårlig test): “Pleier å krysse over.”

Foreleser: Magne Thoresen

Ressurser
Presentasjon

Gruppeøvelser i statistikk

Oppgave 9
1. Forklar hva vi mener med et konfidensintervall. Ta utgangspunkt i den binomiske situasjonen.
Om vi gjentar et forsøk mange ganger, vil et 95% konfidensintervall si at andelen konfidensintervall (basert på en estimert sannsynlighet) som inneholder den sanne populasjonsverdien p er 95%.

Binomisk situasjon: X ~ bin(n, p)
Konfidensintervall: p^ +- 1.96 * sqrt(p^(1-p^)/n) hvor sqrt(p^(1-p^)/n) er den estimerte standardfeilen.

Del 1
1. Gjør de beregningene som er nødvendige for å finne de feilmarginene som er oppgitt over.
Feilmarginene her vil si 1.96 * standardfeilene for et 95% konfidensintervall. Leser av partibarometer og får p^ = 0.297 for Ap og 0.250 for Høyre. Vi finner standardfeil ved Sp = sqrt(p^(1-p^)/n) hvor n er 721. Vi får Sp(Ap) ~= 0.017. 0.017 * 1.96 ~= 0.033. Sp(H) ~= 0.016. 0.016 * 1.96 ~= 0.032

2. Hva skal vi mene med øvre og nedre grense for partitilslutning? Gjør de beregningene som er nødvendig for å finne øvre og nedre grense for Arbeiderpartiet og Høyre. Hva synes du om overskriften til NRK: Dårlig måling for Støre: Ap under 30 prosent
Med øvre og nedre grense mener vi konfidensintervall. Formelen for et 95% konfidensintervall er p^ +- 1.96 * Sp. Vi får for Ap: 0.297 +- 0.033. For høyre får vi: 0.250 +- 0.032. Sannsynligheten for at den sanne oppslutningen for Ap er over 30% er nesten like stor som at den er under. Litt misvisende overskrift.

3. Kan vi bruke tilnærmingen til normalfordelingen i de beregningene vi gjør her? Hvor er det vi bruker den i våre beregninger?
Vi bruker antagelsen når vi regner ut feilmargin og konfidensintervall (øvre/nedre partigrense). Vi kan bruke tilnærmingen pg.a. sentralgrenseteoremet. np og nq er > 5.

Del 2
4. Gi en begrunnelse for at en skulle vente en binomisk fordeling med samme p hvis risikoen for spontanabort var den samme for hver kvinne.

Kvinnene er uavhengig fra hverandre
Vi kan måle om hendelsen spontanabort inntreffer
Sannsynligheten for spontanabort er samme og konstant for hver kvinne

5. Hvilken andel av det totale antallet graviditeter har resultert i spontanabort?
p^ = ((28 + 14 + 15 + 24) = 81) / (70 * 4 = 280) ~= 0.29

6. Beregn et 95% konfidensintervall for andelen spontanaborter. Forklar med ord hva denne betyr. Kan vi bruke tilnærmingen til normalfordelingen her?
p^ ~= 0.29
Sp ~= 0.027
Feilmargin ~= 0.053
95% KI: (0.24, 0.34)
Vi tolker det slik at intervallet (0.24, 0.34) har en 95% for å inneholde den sanne populasjonsverdien p.

Vi kan bruke tilnærming pg.a. sentralgrenseteorem og np & nq > 5.

7. Hvis den binomiske sannsynligheten p settes lik denne andelen, beregn da de forventede antall kvinner med henholdsvis 0, 1, 2, 3 og 4 aborter. Sammenlign med den observerte fordelingen over. Diskuter eventuelle avvik.
(4 0): 0.254 * 70 = 17.78
(4 1): 0.415 * 70 = 29.05
(4 2): 0.254 * 70 = 17.78
(4 3): 0.069 * 70 = 4.83
(4 4): 0.007 * 70 = 0.49

Fra tabellen:
(4 0): 24
(4 1): 28
(4 2): 7
(4 3): 5
(4 4): 6

Vi ser at de forventede tallene vi får ikke stemmer så godt overens med tallene vi observerer. Dette kan tyde på at fordelingen vi har ikke er binomisk og at f.eks. p ikke er lik for alle kvinner.

Oppgave 10
1. Hva er sannsynligheten for at en (tilfeldig valgt) pasient med metabolsk syndrom har hjerte- og karsykdom. Finn et konfidensintervall for denne andelen.
p^ = 29/198 ~= 0.146
Sp ~= 0.025
95% KI: (0.097, 0.195)

2. Beregn differansen i andelen med hjerte- og karsykdom for dem med og uten metabolsk syndrom. Beregn også konfidensintervallet for differansen. Dette må du regne ut for hånd!
p^1 = 0.146
p^2 = 8/73 ~= 0.110
RD = 0.146 – 0.110 = 0.036

Regner ut konfidensintervall:
Finner felles standardfeil Sf = sqrt((p^1 * (1 – p^1) / n1) + (p^2 * (1 – p^2) / n2)) ~= 0.044
95% konfidensintervall er gitt ved: RD +- 1.96 * Sf
Vi får konfidensintervall (-0.05, 0.12).

3. Beregn relativ risiko (RR), med konfidensintervall.
RR = 0.146 / 0.110 ~= 1.33

95% konfidensintervall for RR er definert ved RR * e^(+- 1.96 * SRR) hvor SRR = sqrt(1/29 + 1/8 – 1/198 – 1/73) ~= 0.375. Da får vi konfidensintervall (0.64, 2.77).

4. Beregn også odds ratio (OR), med konfidensintervall.
OR = (29/169) / (8/65) ~= 1.39

95% konfidensintervall for OR er definert ved OR * e^(+- 1.96 * SOR) hvor SOR = sqrt(1/29 + 1/8 + 1/169 + 1/65) ~= 0.425. Da får vi konfidensintervall (0.60, 3.20).

5. Du har i pkt. 2, 3 og 4 beregnet tre alternative mål for effekten som metabolsk syndrom har på hjerte- og karsykdom. Hvilket av disse ville du bruke hvis du skal presentere dette for en gruppe lekfolk?
Alle effektmålene har egne styrker. I denne sammenhengen ville jeg valgt RR eller RD da disse er lettere å forstå. Vi får at en pasient med metabolsk syndrom er ~33% (1.33) mer eksponert for hjerte- og karsykdom. RD forteller oss at den reelle forskjellen er ~3.6%.

6. Sett opp nullhypotesen for å studere om andelene med hjerte- og karsykdom er like for
dem med og uten metabolsk syndrom. Test nullhypotesen. Hvilken konklusjon finner
du?
Vi kan bruke Y-test og Chi-kvadrat-test.

Y-test:
Setter α-nivå = 0.05
H0: p1 = p2
HA: p1 != p2

p^1 ~= 0.146
p^2 ~= 0.110

Finner z-skår, altså Y = (p^1 – p^2) / sqrt(((1/n1)+(1/n2))*p-(1-p-)) hvor p-, den gjennomsnittlige p, = (x1 + x2) / (n1 + n2). Vi får da Y ~= 0.77 som gir i tabellen 0.7794. P-verdi blir da 2*(1 – 0.7794) ~= 0.44. Dette er mye større enn 0.05. Vi kan ikke forkaste H0.

Chi-kvadrat-test:
H0: p1 = p2
HA: p1 != p2

Andel med metabolsk syndrom: 198/271 ~= 0.73
Forventet andel med metabolsk syndrom med hjerte- og karsykdom: 37*0.73 = 27.01
Forventet andel med metabolsk syndrom uten hjerte- og karsykdom: 234*0.73 = 170.82

Andel uten metabolsk syndrom: 73/271 ~= 0.27
Forventet andel uten metabolsk syndrom med hjerte- og karsykdom: 37*0.27 = 9.99
Forventet andel uten metabolsk syndrom med hjerte- og karsykdom: 234*0.27 = 63.18

Vi regner ut teststørrelse X^2:
X^2 = (29 – 27.01)^2 / 27.01 + (169 – 170.82)^2 / 170.82 + (8 – 9.99)^2 / 9.99 + (65 – 63.18)^2 / 63.18 ~= 0.61

Antall frihetsgrader: (kolonner – 1) * (rader – 1) = 1
For α-nivå 0.05 har vi en verdi 3.84. Fordi teststørrelsen vi fant er mye mindre enn 3.84, kan vi ikke forkaste H0.

Oppgave 11
1. Bruk tabellen til å undersøke om andelen med hjerte- og karsykdom avhenger av om personen er overvektig eller ikke. Sett opp en nullhypotese og test den.
Vi kan bruke Y-test og Chi-kvadrat-test.

Y-test:
Setter α-nivå = 0.05
H0: p1 = p2
HA: p1 != p2

p^1 ~= 0.19
p^2 ~= 0.060

Finner z-skår, altså Y = (p^1 – p^2) / sqrt(((1/n1)+(1/n2))*p-(1-p-)) hvor p-, den gjennomsnittlige p, = (x1 + x2) / (n1 + n2). Vi får da Y ~= 6.32 som gir i tabellen > 0.9998. P-verdi blir da < 2*(1 – 0.9998) ~= 0.0004. Dette er mye mindre enn 0.05. Vi kan med god sikkerhet forkaste H0.

Chi-kvadrat-test:
H0: p1 = p2
HA: p1 != p2

Andel med overvekt: 312/994 ~= 0.31
Forventet andel med overvekt med hjerte- og karsykdom: 100*0.31 = 31
Forventet andel med overvekt uten hjerte- og karsykdom: 894*0.31 = 277.14

Andel uten overvekt: 682/994 ~= 0.69
Forventet andel uten overvekt med hjerte- og karsykdom: 100*0.69 = 69
Forventet andel uten overvekt med hjerte- og karsykdom: 894*0.69 = 616.86

Vi regner ut teststørrelse X^2:
X^2 = (60 – 31 )^2 / 31 + (40 – 69)^2 / 69 + (252 – 277.14)^2 / 277.14 + (642 – 616.86)^2 / 616.86 ~= 42.62

Antall frihetsgrader: (kolonner – 1) * (rader – 1) = 1
For α-nivå 0.05 har vi en verdi 3.84. Fordi teststørrelsen vi fant er mye større enn 3.84, kan vi med god sikkerhet forkaste H0.

2. Bruk differansen i andelen med hjerte- og karsykdom som effektmål for effekten av overvekt på hjerte- og karsykdom. Finn et estimat for effekten og lag et konfidensintervall (for hånd!).
p^1 ~= 0.19
p^2 ~= 0.060
RD = 0.19 – 0.060 = 0.13

Regner ut konfidensintervall:
Finner felles standardfeil Sf = sqrt((p^1 * (1 – p^1) / n1) + (p^2 * (1 – p^2) / n2)) ~= 0.024
95% konfidensintervall er gitt ved: RD +- 1.96 * Sf
Vi får konfidensintervall (0.083, 0.18).

3. Bruk relativ risiko som effektmål. Beregn den og finn et konfidensintervall for den.
RR = 0.19 / 0.060 ~= 3.17

95% konfidensintervall for RR er definert ved RR * e^(+- 1.96 * SRR) hvor SRR = sqrt(1/60 + 1/40 – 1/312 – 1/682) ~= 0.19. Da får vi konfidensintervall (2.18, 4.60).

4. Bruk odds ratio som effektmål, beregn den og finn konfidensintervallet.
OR = (60/252) / (40/642) ~= 3.82

95% konfidensintervall for OR er definert ved OR * e^(+- 1.96 * SOR) hvor SOR = sqrt(1/60 + 1/40 + 1/252 + 1/642) ~= 0.22. Da får vi konfidensintervall (2.48, 5.88).

5. Les inn tabellen over i SPSS. Lag variabelnavn, variabel labels og value labels og
presenter selve tabellen.
Kommer senere

6. Beregn RR, OR med tilhørende konfidensintervall ved å bruke SPSS.
Kommer senere

7. Hvordan vil du presentere sammenhengen mellom overvekt og hjerte- og karsykdom, og hvordan vil du konkludere om sammenhengen mellom overvekt og hjerte- og karsykdom?
Alle effektmålene har egne styrker. I denne sammenhengen ville jeg valgt RR eller RD da disse er lettere å forstå. Vi får at en pasient med overvekt er ~317% (3.17) mer eksponert for hjerte- og karsykdom. RD forteller oss at den reelle forskjellen er ~13%. Vi ser at om H0 for RR = 1 og RD = 0, er ingen av disse inkludert i deres tilsvarende 95% konfidensintervall. Vi kan si med 95% sikkerhet at det er en betydelig sammenheng mellom overvekt og økt forekomst av hjerte- og karsykdom.

Foreleser: Simon Lergenmuller

Ressurser
Oppgaver

Gruppeøvelser i statistikk

Oppgave 3
En (europeisk) rulett har 37 felter, som er nummerert 0 og 1 til 36. Feltet 0 har fargen grønn, 18 er røde og 18 er sorte. For mer informasjon, se http://no.wikipedia.org/wiki/Rulett. Croupieren (spillelederen) spinner hjulet og ruller en liten ball langs hjulet i motsatt retning. Hjulet er balansert slik at det er like sannsynlig å lande på alle feltene. Spillerne kan spille på alle kombinasjoner av tall og farger.

1. Hva er sannsynlighetene for å falle i hvert av feltene?
1/37

2. En spiller som spiller på rødt, vinner hvis ballen lander på et rødt felt. Hva er sannsynligheten for dette?
18/37

3. Spillekasinoet har bestemt at dersom kulene lander på feltet 0 (”huset vinner”), går innsatsen til spillerne til spillekasinoet. Hva er sannsynligheten for at spillekasinoet skal få innsatsen til en spiller?
1/37 P for at kulen lander på 0
19/37 for å tape gitt at sats på 0 ikke er mulig

4. Du går i spillekasinoet en kveld og bestemmer deg for å spille 20 ganger. Hver gang satser du 1000 kroner og hele tiden satser du på rødt. Hver gang kulen lander på sort eller på 0, går pengene dine til spillekasinoet, og hver gang det blir rødt, får du igjen det dobbelte av det du satset. Kan du forvente å vinne på dette spillet? Hvis ikke, hvor mye vil du i så fall måtte forvente å tape?
E(r) = 18/37 * 20 = 9.73
E(ir) = 19/37 * 20 = 10.27

Vi ser at andelen spill vi kan forvente å vinne blir mindre etterhvert som vi spiller flere spill. Om vi spiller 20 ganger kan vi forvente å vinne ~48.65% av gangene, altså 9.73 eller ~10 spill. Likeså forventer vi å tape ~51.35% av gangene, altså 10.27 eller ~ 10 spill. Ettersom vi bare kan spille “hele spill”, kan vi si at vi forventer å gå i null, men at sannsynligheten for at vi taper er større enn at vi vinner.

5. En annen spiller har observert at det har kommet rødt seks ganger etter hverandre. Han synes dette er mistenkelig og konkluderer med at ”rødt er i skuddet”, og vil fra da av satse bare på rødt. Hvis spillet er «rettferdig» i den forstand at sannsynligheten er som vi antok i pkt. 2, hva er da sannsynligheten for at kulen skal falle på rødt 6 ganger etter hverandre?
P(6rød) = (18/37)^6 ~= 0.013 = 1.3%

6. Spilleren mener at sannsynligheten for å falle på rødt kanskje kan være så høy som 0.6, siden kulen faller så ofte på rødt. Hva er sannsynligheten for at det skal komme rødt seks ganger hvis sannsynligheten er 0.6?
P(6rød) = (0.6)^6 ~= 0.047 = 4.7%

7. Spilleren vil gå til spillelederen og si at spillet ikke er rettferdig. Hva vil du si til denne spilleren? For å begrunne svaret ditt kan du tenke deg at spillelederen i løpet av en kveld rekker å spille 1000 sekvenser à 6 spill. Hvor mange av disse sekvensene kan vi forvente vil gi 6 røde på rad, når spillet er «rettferdig»?
P(6rød) ~= 0.013.
E(x) = 0.013*1000 = 13 sekvenser

Oppgave 4
En meteorolog som er ansatt på Værnes har fått gjentatte klager fordi han ikke klarer å treffe med værmeldingene sine. For å vurdere kvaliteten på det utførte arbeidet har sjefen hans laget en tabell med observerte frekvenser for hva meteorologen meldte og det det været som faktisk ble observert.

Bruk sannsynlighetsregnereglene vi har lært til å svare på følgende spørsmål:

1. Hva er sannsynligheten for sol?
Addisjonsregelen.
P(S) = 0.3 + 0.05 + 0.05 = 0.4 = 40%

2. Hva er sannsynligheten for at meteorologen tar feil?
Komplementsetningen.
P(F) = P(iR) = 1 – P(R) = 1 – (0.3+0.2+0.2) = 1 – (0.7) = 0.3 = 30%

3. Hva er sannsynligheten for at for det kommer regn når meteorologen sier det blir sol?
P(R|OS) = 0.1 / 0.44 ~= 0.23 = 23%

Oppgave 5
Vi er interessert i å se på sammenhengen mellom en test og en sykdom for å undersøke testens evne til å skille mellom syke og friske. Vi ser på et utvalg av 50.000 personer som har blitt testet for en bestemt sykdom. Av disse har 100 sykdommen. Av de 100 som har sykdommen er det 95 som får positivt testresultat. Av de som er friske er det 48902 personer som får negativt testresultat.

1. Sett opp en tabell som viser antall syke/friske med positiv/negativ test.

2. Hva er sannsynligheten i dette utvalget for å ha sykdommen?
Prevalens = 100 / 50000 = 1/500 = 0.002 = 0.2%

3. Hva er testens sensitivitet og spesifisitet, og hva betyr dette i ord?
Sensitivitet = P(P|S) = 95 / 100 = 95%
Spesifisitet = P(N|F) = 48902 / 49900 = 98%
*Har stått feil her tidligere (50000)

4. Hva er den positive prediktive verdi av testen? Hva betyr dette i ord, og hva betyr dette for testens praktiske verdi?
PPV = P(S|P) = 95 / 1093 ~= 0.087 = 8.7%
Når bare 8.7% av de positive utslagene er riktige er det nok ikke lurt å bruke testen som veiledende for pasientbehandling.

5. Finn også hva negativ prediktiv verdi av testen er.
NPV = P(F|N) = 48902 / 48907 ~= 0.999 = 99.9%
Ettersom PPV er lav, men NPV høy, er det rimelig å anta at testens styrke ligger i å minske utvalget ved å kjemme bort de som i allefall ikke er syke, altså de friske. Når det er gjort kan vi gjøre en annen diagnostisk test med høyere PPV, men kanskje lavere NPV.

6. Sett også opp positiv prediktiv verdi og negativ prediktiv verdi ved hjelp av Bayes regel.
PPV
P(S) = Prevalens = 0.002
P(P) = 1093 / 50000 ~= 0.022
P(P|S) = Sensitivitet ~= 0.95
P(S|P) = (P(S) / P(P)) * P(P|S) = (0.002 / 0.024) * 0.95 ~= 0.086 = 8.6%

NPV
P(F) = 49900 / 50000 = 0.998
P(N) = 48907 / 50000 ~= 0.978
P(N|F) = Spesifisitet ~= 0.978
P(F|N) = (P(F) / P(N)) * P(N|F) = (0.998 / 0.978) * 0.978 = 0.998 = 99.8%

7. Hvis vi i stedet tester utsatte risikogrupper, øker sannsynligheten for sykdommen til 5%. Testens sensitivitet og spesifisitet er den samme som du fant i pkt. 3 over. Hva skjer med positiv prediktiv verdi hvis vi ser på 50.000 personer med utsatt risiko for sykdommen?
PPV øker.

Vi ser på en annen type test, der sannsynligheten for å ha sykdommen i utsatte land er 10%. Sannsynligheten for at testen er positiv når man er smittet av sykdommen er 0.999 og sannsynligheten for at testen er negativ når man ikke er smittet er 0.99.

8. Hva er testens sensitivitet og spesifisitet?
Sensitivitet = P(P|S) = 0.999
Spesifisitet = P(N|F) = 0.99

9. Hva blir positiv prediktiv verdi? Bruk Bayes regel.
P(S) = Prevalens = 10%
PPV = Sensitivitet * Prevalens / (Sensitivitet * Prevalens + (1 – Spesifisitet) * (1 – Prevalens)) = 0.999 * 0.1 / (0.999 * 0.1 + (1 – 0.99) * (1 – 0.1)) ~= 0.92 = 92%

10. På verdensbasis er sannsynligheten for å ha sykdommen 1%. Hvis testens sensitivitet og spesifisitet er den samme, hva blir da positiv prediktiv verdi?
P(S) = 1%
PPV = Sensitivitet * Prevalens / (Sensitivitet * Prevalens + (1 – Spesifisitet) * (1 – Prevalens)) = 0.999 * 0.01 / (0.999 * 0.01 + (1 – 0.99) * (1 – 0.01)) ~= 0.50 = 50%

11. Ser du en sammenheng mellom prevalensen av sykdommen og positiv prediktiv verdi?
Ja.
ref

Foreleser: Morten Valberg

Ressurser
Oppgaver

Binomisk fordeling

Hovedsakelig en presentasjon med utdypning.

Eksempler på begivenheter som kan være ikke-uavhengige:

Gjentatte observasjoner av samme subjekt
Slektskap mellom individer (genetisk predisposisjon)
Smittsomme sykdommer

Binomisk fordeling
For å kunne ta i bruk binomiske fordelinger må vi innfri visse krav:

Begivenhetene må være uavhengige
Begivenhetene må være binære (to utfall)
Sannsynlighetene for utfallene må være statiske

Hvor mange vil vi forvente?
E(X) – forventning til X
n – totalmengden
P – sannsynlighet for X

E(X) = n*P

Standardavvik
SD(X) – Standard deviation of X (Standardavviket til X)
n – totalmengden
p – sannsynlighet for X

Mer om dette

Foreleser: Magne Thoresen

Ressurser
Presentasjon

Bayes lov

Bayes lov er typisk den regneregelen som blir gitt mest på eksamen. Ikke tolk det som at de andre formlene overhodet ikke kan gis. Vi bruker Bayes formel bl.a. når vi skal beregne usikkerhet i diagnostiske tester (HIV, mammografi, HCG (graviditetstest).

Sensitivitet
Sannsynligheten for at en test slår positivt (P) gitt at personen er syk (S). Med andre ord, sannsynligheten for at testen gir et positiv utslag når du er syk.

Spesifisitet
Sannsynligheten for at en test slår negativt (iP) gitt at personen er frisk (iS). Med andre ord, sannsynligheten for at testen gir et negativt utslag når du er frisk.

Positiv prediktiv verdi
Sannsynligheten for at en person er syk (S) gitt et positivt utslag (P). Med andre ord, sannsynligheten for at du faktisk er syk dersom testen har gitt et positivt uslag.

Negativ prediktiv verdi
Sannsynligheten for at en person er frisk (iS) gitt et negativt utslag (iP). Med andre ord, sannsynligheten for at du faktisk er frisk dersom testen har gitt et negativt utslag.

Denne bør være høy. Dersom en stor del av de negative utslagene er feil kan vi oppleve å ende opp med grupper som er syke, men som tror de er friske (og systemet). Dette er farlig bl.a. fordi de da fortsetter ubehandlet (dårlig for dem selv) og eventuelt fører smitten videre til andre (dårlig for samfunnet).

Prediktive verdier er avhengig av prevalensen til diagnosen. Ved lav prevalens går PPV ned. Det vil si at sannsynligheten for at en positiv test faktisk viser riktig blir mindre. En lav PPV er spesielt aktuelt ved masseundersøkelser. Vi kan ende opp med at de fleste av personene med positiv prøve faktisk er friske! Derfor er det viktig med høy spesifisitet, da i allefall de negative utslagene vil være å stole på.

Forklaring på forhold mellom sensitivitet og spesifisitet, og PPV og NPV.
Anta teoretisk sensitivitet = 0.9.
Anta teoretisk spesifisitet = 0.9.

Sensitivitet sier at medisinen har en 90% sjanse for å riktig si at du er syk, men også 10% sjanse for å si at du er feilaktig frisk (syk person er frisk). Spesifisitet sier at medisinen har en 90% sjanse for å riktig si at du er frisk, men også 10% sjanse for at du er feilaktig syk (frisk person er syk). Det er en grunn til at det heter sykdom, så det vil i nesten alle tilfeller være mange flere som er friske. Dersom spesifisiteten ikke er høy nok, vil de 10% som får et feilaktig positivt utslag på at de er syke være flere enn de 90% som får et riktig et. Med andre ord, vil antall feilaktig positive utslag være større enn antall riktig positive utslag, dvs. at antallet friske vil være større enn faktisk syke blant de med positive utslag. 10% av 1000 er 100, mens 90% av 10 er 9. PPV = 9/109 ~= 0.083 = 8.3%. Så av de som får positivt utslag er bare 8.3% faktisk syke.

Det er derfor vi sier at prediktive verdier er avhengig av prevalens. Dersom vi øker antall syke i testutvalget, dvs. at 90% er 1000, vil vi få en høyere PPV. Dette går imidlertid på bekostning av en lavere NPV dersom sensitiviteten forblir den samme. Flere syke, men samme sensitivitet vil si at vi får flere faktisk syke, men også flere feilaktig friske. Antall feilaktig friske er en faktor i NPV, mens antall faktisk syke er en faktor i PPV.

Mange diagnostiske tester baserer seg på en grenseverdi som bestemmer definisjonen på friske og syke. Dersom grenseverdien blir lagt til 0, vil i praksis ALLE bli diagnostisert som syke (alle under 0 er friske, alle over 0 er syke). Alle som er syke vil få et positivt utslag, dvs. at sensitiviteten er 100%. På den andre siden vil ingen få et utslag som er negativt, og spesifisiteten derfor 0%. Det vil være balansegang mellom høy spesifisitet og høy sensitivitet. Hva som er viktigst / hvilke verdier som er fornuftige avhenger av situasjonen.

Det er en del regneeksempler i presentasjonen.

Foreleser: Magne Thoresen

Ressurser
Presentasjon

Sannsynlighetsregning II

I læren om sannsynligheter finner vi blant annet en tanke om tilfeldige forsøk. Når vi leder slike forsøk vet vi ikke på forhånd hva utfallet vil bli. Vi kjenner kun til mulighetene (utfallsrommet, S). Eksempler på når dette gjelder kan være:

Myntkast (S = {Kron, Mynt})
Kategorisk data
Diskret utfallsrom
Terningkast (S = {1, 2, 3, 4, 5, 6})
Kategorisk data
Diskret utfallsrom
Banefødsler (S = {Jente, Gutt})
Kategorisk data
Diskret utfallsrom
Telle antall lungekrefttilfeller i Oslo i løpet av et år (S = {ℕ₀})
Diskrete numeriske data (telletall)
Diskret utfallsrom
Kreftbehandling. Hvor lenge lever pasienten? (S = { ${\mathbb {R}}_{{>0}}$ })
Kontinuerlig data
Kontinuerlig utfallsrom

Vi er ofte i sannsynlighetsregning ute etter sannsynligheter for forskjellige delmengder, eller begivenheter innen et gitt utfallsrom. Når vi gjør forsøk bruker vi begrepet serie for å betegne en rekke likeartede forsøk (samme konsept som sets og reps på Domus Athletica).

Hva er sannsynlighet?
Det er ofte snakk om to tolkninger som svar til spørsmålet:

Frekventistisk
Dette beskriver typen sannsynlighet vi er vant med. F.eks. at sannsynligheten for at en terning lander på 6 blir nærmere og nærmere 1/6 jo flere forsøk vi gjør. Skrevet på en ordentlig måte:
La antall kast i hver serie være N og antall ganger terningen lander på 6 være nA. Den relative frekvensen til A, fA, er andelen kast som lander på 6. Det vil si antall ganger terningen lander på 6, nA, delt på antall totale kast, N: nA/N. Sannsynligheten for A, P(A), nærmer seg den relative frekvensen, fA, når antall kast, N, nærmer seg uendelig.Forenklet: Jo flere kast, jo nærmere kommer vi en “teoretisk sannsynlighet” for at terningen lander på 6.Eksempel
Vi kaster en terning først 12 ganger. Da forventer vi å få 1/6*12 = 2 seksere. Når vi kaster får vi i stedet 4 seksere. Om vi regner ut sannsynligheten utifra dette får vi at sannsynligheten for seksere blir P(6) = 4/12 = 1/3 i stedet. Så kaster vi terningen 120 ganger og får 16 seksere. P(6) = 16/120 = 4/30. 1/6 = 5/30. Her ser vi hvordan den relative frekvensen (praktisk resultat) nærmer seg den teoretiske sannsynligheten ettersom vi kaster flere kast.
Bayesiansk
Dette beskriver en type sannsynlighet som er basert på forventninger i forkant av forsøket og er sannsynligvis ikke pensum.

Vi har (minst) fem grunnleggende regneregler som vi skal lære nå:
U (union) betyr eller
∩ (snitt) betyr og

Komplementsetningen

Sannsynligheten for A og ikke A legges sammen til 1.
Addisjonssetningen for disjunkte hendelser

To disjunkte hendelser har ingenting å gjøre med hverandre. Si at i et klasserom finner vi 50% som shipper Barney og Robin og 30% som shipper Ted og Robin med ingen overlapping. Da er det naturlig at sannsynligheten for at en tilfeldig valgt elev i klassen shipper Robin med enten Barney eller Ted vil være 50% + 30% = 80%. Sannsynligheten for at en i klassen shipper Robin med både Barney og Ted vil på den andre siden være 0, fordi vi vet at ingen gjør det. Tomme mengder merker vi ofte med Ø. P(B∩T) = Ø.
Addisjonssetningen

Se for deg et venndiagram. Når to hendelser ikke er disjunkte og har overlapp ser vi at om vi teller sannsynlighetene P(A) og P(B), eller sirklene A og B, hver for seg, vil vi telle med området der det overlappes to ganger. Derfor må vi trekke det fra en gang. Fellesarealet noteres P(A∩B).
Produktsetningen

Dersom hendelsene A og B skal begge inntreffe, må B inntreffe først for at A skal kunne inntreffe. Dersom sannsynligheten for at A inntreffer er avhengig om B inntreffer eller ikke, kan sannsynligheten regnes utifra multiplikasjonssetningen (produktsetningen).
For uavhengige hendelser gjelder

Dersom sannsynligheten for at A inntreffer er uavhengig av B vil P(A|B) i praksis være det samme som P(A).P(A|B) er et eksempel på betinget sannsynlighet. Det handler om å finne sannsynligheten for at A kommer til å skje dersom B allerede har skjedd. Eksempel: Sannsynligheten for Robin blir sammen med Ted dersom Barney har dødd.

For å friske opp litt kunnskap fra videregående kan det være lurt å sjekke ut matematikk.net. Det er flere eksempler i presentasjonen.

De første forelesningene er for å bygge opp det grunnleggende og kan selvsagt oppleves som kjedelige. Foreleser ønsker at studentene kikker litt på oppgavesettet til gruppearbeidet i morgen (fredag).

LIK står for Legestudentenes Idrettsklubb og er, ja, en idrettsklubb. Medlemskap koster kr 10. Studentlekene arrangeres 10. oktober. Det er bare å stille lag!

Foreleser: Magne Thoresen

Ressurser
Presentasjon